The factors that define your chance of winning the lottery

In this article, we will explain:

• how lotteries work
• how lotteries generate a profit
• what your chances are of winning any specific prize at the lottery
• how the math behind the lottery works
• the concept of profit expectation, also known as Expected Value
• how do take all those factors into account to decide which lottery to play, and when to buy a ticket

How do lotteries generate profits?

Simply put, all lotteries make a profit by making sure that only a percentage of the money coming in through ticket sales will be paid out in the form of winnings. To make a profit, the payouts in all the winning tiers have to be considered, from the jackpot down to the smallest possible win.

Most state-run lotteries have relatively high margins. The two main reasons for that are:

1. They have relatively high operational and administration expenses
2. Their profits are being used to support all kinds of welfare projects, or other endeavors that are in the public interest. Those can be amateur sports, environmental projects, etc. Instead of using tax revenues to fund such projects, states often hold lotteries to come up with the necessary funds. You could even say that lotteries are a form of “voluntary” taxation.

What defines the chances of winning for the players?

Let’s look at the math behind the concept of lottery. In every winning tier, your chances are defined by the number of possible outcomes of the draw, or the odds. Those odds are often given as 1 in X – X being the number of possible outcomes. But by dividing 1 by X, you can also come up with those odds as a percentage.

For example, if you roll a dice, there are six possible outcomes. Guessing the result of any roll would give you a 1 in 6 chance. You could also divide 1 by 6, and you would get a 16,667% chance of guessing the right outcome.

At the same time, you also need to consider the amount you can win, and the price you pay to participate. Let’s take a close look at this concept.

The concept of Profit Expectation, or Expected Value

Let me use a simple example to explain what Expected Value is. We will use the abbreviation EV here.

Let’s say I flip a coin, and pay you $1 every time the coinflip result is heads. But every time the result is tails, you have to pay me $1. If we were to do this many, many times, the EV would get close to zero, right?

But what if I were to pay you $2 every time you win, and you pay me $1 every time you lose? Well, that would mean that you make a profit in the long run. Flip the coin a thousand times, the outcome would be approximately 500 times heads (you win $1000) and 500 times tails (you lose $500). That is a profit of $500 for 1000 coinflips, or $0,50 per coinflip.

How can we apply this to the lottery?

Assuming a fixed ticket price (we can use $1 as the price for one entry to the lottery here), we have to calculate this as follows:

The percentage chance, multiplied by the amount you would win = Your expected value

If we want to know how this applies to winning the jackpot, this is how we do it. Let’s use Mega Millions as an example. The odds of winning the jackpot here are 1 in 302.575.350, which means a percentage of 0,00000033049619%. The other factor is the size of the jackpot, which of course varies. The following table shows how your EV depends on the size of the jackpot.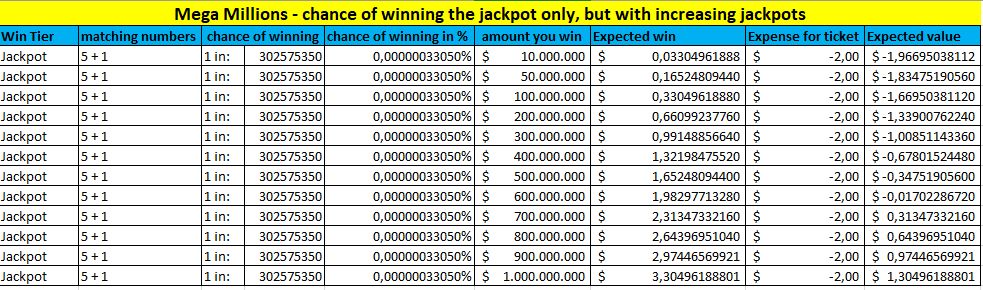

This is interesting, right? You can see that mathematically, your EV increases as the jackpot increases. Actually, in that table, you can see that when the jackpot is at $ 700 million, your EV is roughly $0,31. And this number does not even take into account your chances of winning any of the other prizes in the lower tiers.

That leads us to another interesting thought. Assuming the jackpot is at $700 million, and there are 302,575 million possible number combinations. What if we were to buy 302,575 million tickets, at the price of $2,00, to cover all possible number combinations? That would cost us roughly $605 million, but we would have a guaranteed win of $700 million plus all the smaller wins. That should work, right? Unfortunately, this will not work, even if you were to have the money to buy this many lottery tickets.

So why is this not a viable strategy to win every time?

Two simple reasons:

• Taxes – if you do win, you will have to pay at least 30% taxes on your winnings. That means that the jackpot has to be even higher than what the table suggests, for you to have a guaranteed profit.
• Multiple winners will split the jackpot – you may be guaranteed to win the jackpot, but what if one or two more people have the winning numbers? You would have to split the jackpot, but the amount you win is not guaranteed. And then, there is still the tax issue.

Comparing the Expected Value for the biggest lotteries

Now we will take a look at which lotteries offer the “best deal” for your money. We will compare our top-selling lotteries, which are Mega Millions, Powerball, Euromillions, and Eurojackpot. To be able to provide a fair comparison, we will assume that the jackpot is the same for each lottery, at 100 million.

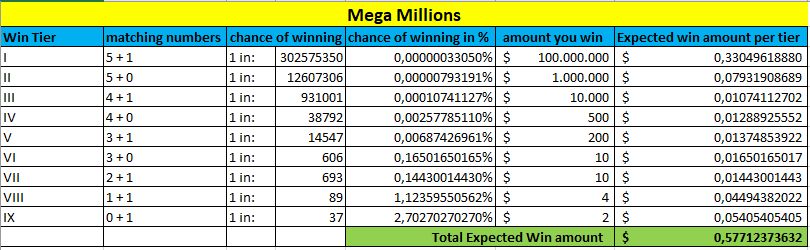
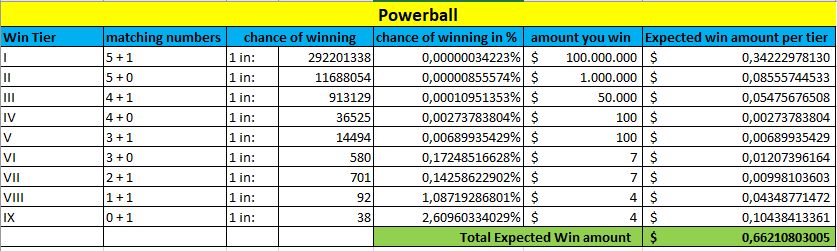
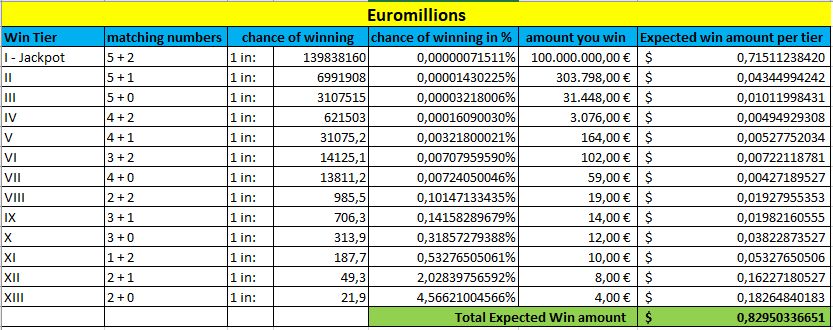
Also, now we will take into account all prize tiers and their probabilities, combined with the average amount you can expect in each tier.

At the bottom of each table, marked in green, you can see the Expected Win amount. The higher this amount is, the better your chances are to win this lottery.

Mega Millions

Powerball

Euromillions

Eurojackpot

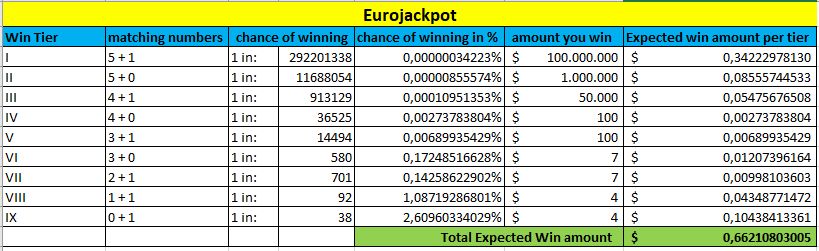
Again, all this changes when the jackpots increase. But the above table gives you a good comparison of the lotteries in general, based on your odds of winning any prize.

Conclusion

Not all lotteries offer the same odds of winning. While the various lotteries all work in the same way basically, every lottery has a different structure of pay-outs and winnings.

But at the end of the day, the one thing that makes sense is that the higher the jackpot is, the more reason you have to get a ticket and participate in the lottery!