I denne artikkelen vil vi forklare:
- hvordan lotterier fungerer
- hvordan lotterier genererer fortjeneste
- hva sjansene dine er for å vinne en bestemt premie i lotteriet
- hvordan matematikken bak lotteriet fungerer
- begrepet forventet gevinst, også kjent som forventet verdi (Expected Value)
- hvordan du tar hensyn til alle disse faktorene når du bestemmer deg for hvilket lotteri du skal spille, og når du skal kjøpe lodd
Hvordan genererer lotterier fortjeneste?
Enkelt sagt går alle lotterier med overskudd ved å sørge for at bare en prosentandel av pengene som kommer inn gjennom loddsalget, blir utbetalt i form av gevinster. For å gå med overskudd må man ta hensyn til utbetalingene på alle gevinstnivåene, fra jackpotten og ned til den minste mulige gevinsten.
De fleste statlige lotterier har relativt høye marginer. De to viktigste grunnene til det er:
- De har relativt høye drifts- og administrasjonskostnader
- Overskuddet brukes til å støtte alle slags velferdsprosjekter eller andre tiltak som er i allmennhetens interesse. Det kan være amatøridrett, miljøprosjekter osv. I stedet for å bruke skatteinntekter til å finansiere slike prosjekter, avholder stater ofte lotterier for å skaffe de nødvendige midlene. Man kan til og med si at lotterier er en form for «frivillig» beskatning.
Hva definerer vinnersjansene for spillerne?
La oss se på matematikken bak lotterikonseptet. I hver vinnerrekke defineres vinnersjansene dine av antall mulige utfall av trekningen, eller oddsen. Disse oddsene oppgis ofte som 1 av X – X er antall mulige utfall. Men ved å dele 1 på X kan du også få oddsen i prosent.
Hvis du for eksempel kaster en terning, er det seks mulige utfall. Hvis du gjetter resultatet av et kast, får du en sjanse på 1 av 6. Du kan også dele 1 på 6, og da får du 16,667 % sjanse for å gjette riktig utfall.
Samtidig må du også vurdere hvor mye du kan vinne, og prisen du betaler for å delta. La oss se nærmere på dette konseptet.
Konseptet gevinstforventning eller forventet verdi
La meg bruke et enkelt eksempel for å forklare hva forventet verdi er. Vi bruker forkortelsen EV her.
La oss si at jeg slår kron og mynt og betaler deg 1 dollar hver gang resultatet er kron. Men hver gang resultatet er kron, må du betale meg 1 dollar. Hvis vi skulle gjøre dette mange, mange ganger, ville EV nærme seg null, ikke sant?
Men hva om jeg betaler deg 2 dollar hver gang du vinner, og du betaler meg 1 dollar hver gang du taper? Vel, det ville bety at du tjener penger i det lange løp. Hvis du kaster mynten tusen ganger, vil utfallet bli ca. 500 ganger kron (du vinner 1000 dollar) og 500 ganger mynt (du taper 500 dollar). Det gir en gevinst på 500 dollar for 1000 myntkast, eller 0,50 dollar per myntkast.
Hvordan kan vi overføre dette til lotto?
Hvis vi går ut fra en fast billettpris (her kan vi bruke 1 dollar som pris for ett lodd i lotteriet), må vi beregne dette på følgende måte:
Den prosentvise sjansen, multiplisert med beløpet du ville vunnet = din forventede verdi.
Hvis vi vil vite hvordan dette gjelder for å vinne jackpotten, gjør vi det på denne måten. La oss bruke Mega Millions som eksempel. Oddsen for å vinne jackpoten her er 1 til 302.575.350, noe som betyr en prosentandel på 0,00000033049619%. Den andre faktoren er størrelsen på jackpoten, som selvsagt varierer. Følgende tabell viser hvordan din EV avhenger av størrelsen på jackpotten.Megamillions jackpot EV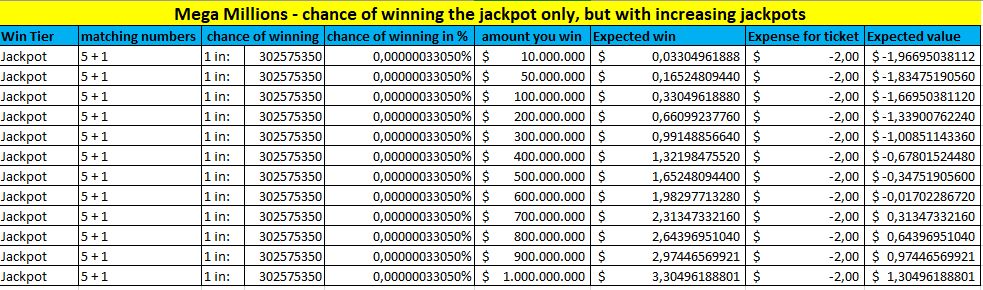
Dette er interessant, ikke sant? Du kan se at matematisk sett øker din EV etter hvert som jackpotten øker. I denne tabellen kan du faktisk se at når jackpoten er på 700 millioner dollar, er din EV omtrent 0,31 dollar. Og dette tallet tar ikke engang hensyn til sjansene dine for å vinne noen av de andre premiene i de lavere nivåene.
Det fører oss til en annen interessant tanke. La oss anta at jackpoten er på 700 millioner dollar, og at det er 302,575 millioner mulige tallkombinasjoner. Hva om vi skulle kjøpe 302 575 millioner lodd til en pris av 2,00 dollar for å dekke alle mulige tallkombinasjoner? Det ville koste oss rundt 605 millioner dollar, men vi ville ha en garantert gevinst på 700 millioner dollar pluss alle de mindre gevinstene. Det burde fungere, ikke sant? Dessverre vil det ikke fungere, selv om du skulle ha penger til å kjøpe så mange lodd.
Så hvorfor er ikke dette en levedyktig strategi for å vinne hver gang?
Av to enkle grunner:
- Skatt – hvis du vinner, må du betale minst 30 % skatt på gevinsten. Det betyr at jackpotten må være enda høyere enn det tabellen antyder for at du skal være garantert en gevinst.
- Flere vinnere må dele jackpotten – du er kanskje garantert å vinne jackpotten, men hva om en eller to personer til har vinnertallene? Da må du dele jackpoten, men beløpet du vinner er ikke garantert. Og så er det fortsatt skattespørsmålet.
Sammenligning av forventet verdi for de største lotteriene
Nå skal vi se på hvilke lotterier som gir deg «mest igjen» for pengene. Vi skal sammenligne de mest solgte lotteriene, som er Mega Millions, Powerball, Euromillions og Eurojackpot. For å kunne gi en rettferdig sammenligning vil vi anta at jackpoten er den samme for hvert lotteri, nemlig 100 millioner.
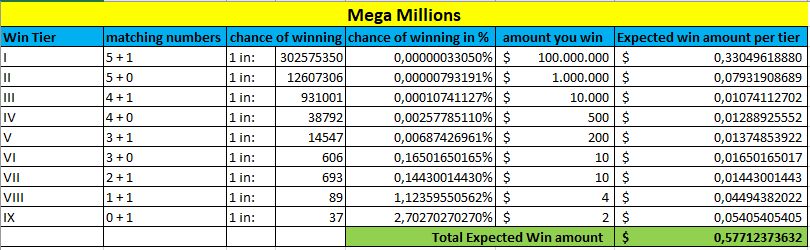
Nå vil vi også ta hensyn til alle premienivåer og sannsynligheten for dem, kombinert med det gjennomsnittlige beløpet du kan forvente i hvert nivå.
Nederst i hver tabell, merket med grønt, kan du se det forventede gevinstbeløpet. Jo høyere dette beløpet er, jo bedre er sjansene dine for å vinne dette lotteriet.
Mega Millions
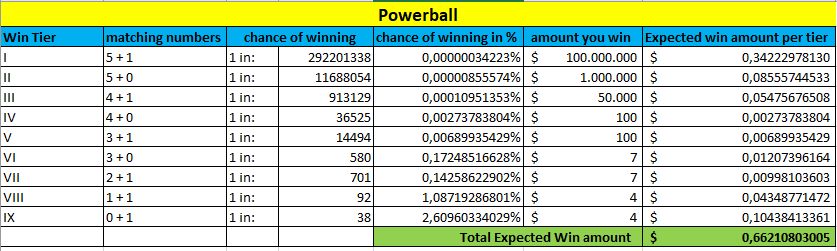
Powerball
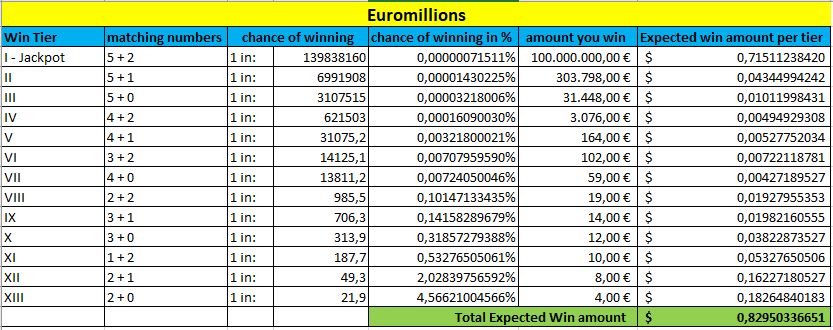
Euromillions
Eurojackpot
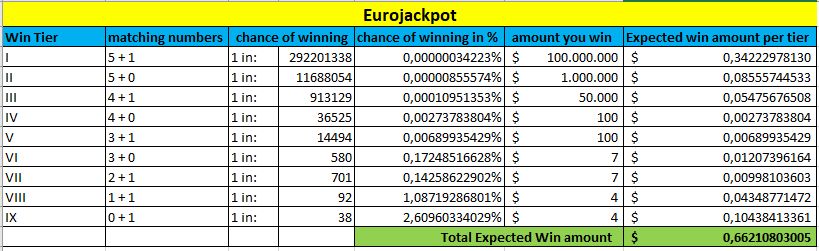
Igjen, alt dette endrer seg når jackpottene øker. Men tabellen ovenfor gir deg en god sammenligning av lotteriene generelt, basert på oddsen for å vinne en premie.
Konklusjon
Ikke alle lotterier tilbyr de samme vinnersjansene. Selv om de ulike lotteriene i utgangspunktet fungerer på samme måte, har hvert lotteri en annen struktur for utbetalinger og gevinster.
Men når alt kommer til alt, er det én ting som gir mening: Jo høyere jackpotten er, desto større grunn har du til å kjøpe en kupong og delta i lotteriet!
