Šajā rakstā mēs izskaidrosim:
- kā darbojas loterijas
- kā loterijas rada peļņu
- kādas ir jūsu izredzes laimēt kādu konkrētu loterijas balvu.
- kā darbojas loterijas matemātika
- paredzamās peļņas jēdzienu, kas pazīstams arī kā paredzamā vērtība (Expected Value)
- kā ņemt vērā visus šos faktorus, lai izlemtu, kurā loterijā spēlēt un kad iegādāties biļeti.
Kā loterijas gūst peļņu?
Vienkāršāk sakot, visas loterijas gūst peļņu, nodrošinot, ka laimestu veidā tiek izmaksāta tikai procentuālā daļa no naudas, kas ienāk no biļešu pārdošanas. Lai gūtu peļņu, ir jāņem vērā visu laimestu līmeņu izmaksas, sākot no džekpota līdz pat mazākajam iespējamajam laimestam.
Lielākajai daļai valsts pārvaldīto loteriju ir salīdzinoši augstas peļņas normas. Tam ir divi galvenie iemesli:
- Tām ir salīdzinoši augstas darbības un administratīvās izmaksas
- to peļņa tiek izmantota, lai atbalstītu visdažādākos labklājības projektus vai citus pasākumus, kas ir sabiedrības interesēs. Tie var būt amatieru sports, vides projekti utt. Tā vietā, lai šādus projektus finansētu no nodokļu ieņēmumiem, valstis bieži rīko loterijas, lai iegūtu nepieciešamos līdzekļus. Varētu pat teikt, ka loterijas ir “brīvprātīga” nodokļu uzlikšanas veids.
Kas nosaka spēlētāju izredzes laimēt?
Aplūkosim loterijas jēdziena matemātiku. Katrā laimestu lozē jūsu izredzes nosaka izlozes iespējamo iznākumu skaits jeb izredzes. Šīs izredzes bieži vien tiek noteiktas kā 1 pret X – X ir iespējamo iznākumu skaits. Bet, dalot 1 ar X, šīs izredzes var izteikt arī procentos.
Piemēram, ja metat kauliņu, ir seši iespējamie iznākumi. Ja uzminēsiet jebkura metiena rezultātu, jums būs iespēja 1 pret 6. Varētu arī dalīt 1 ar 6, un iegūtu 16,667 % iespēju uzminēt pareizo iznākumu.
Vienlaikus jāņem vērā arī summa, ko varat vinnēt, un cena, ko maksājat, lai piedalītos. Aplūkosim šo jēdzienu tuvāk.
Peļņas prognozes jeb paredzamās vērtības jēdziens
Ļaujiet man izmantot vienkāršu piemēru, lai paskaidrotu, kas ir sagaidāmā vērtība. Šeit izmantosim saīsinājumu EV.
Pieņemsim, ka es metu monētu un maksāju jums 1 ASV dolāru katru reizi, kad monētas mešanas rezultāts ir galva. Bet katru reizi, kad rezultāts ir “astīte”, jums ir jāmaksā man 1$. Ja mēs to darītu daudzas, daudzas reizes, EV tuvojas nullei, vai ne?
Bet ko tad, ja es jums maksātu 2 dolārus katru reizi, kad jūs vinnējat, un jūs man maksātu 1 dolāru katru reizi, kad zaudējat? Tas nozīmētu, ka ilgtermiņā jūs gūstat peļņu. Metot monētu tūkstoš reižu, iznākums būtu aptuveni 500 reižu “ar galvu” (jūs vinnējat 1000 dolāru) un 500 reižu “ar astes” (jūs zaudējat 500 dolāru). Tas nozīmē, ka 1000 monētu metienu laikā peļņa ir 500 dolāru jeb 0,50 dolāri par katru monētas metienu.
Kā mēs to varam attiecināt uz loteriju?
Pieņemot, ka biļetes cena ir fiksēta (šeit mēs varam izmantot 1 dolāru kā cenu par vienu loterijas biļeti), mums tas jāaprēķina šādi:
Procentuālā iespēja, reizināta ar summu, ko jūs varētu vinnēt, = jūsu paredzamā vērtība.
Ja mēs vēlamies uzzināt, kā tas attiecas uz laimestu, mēs to darām šādi. Kā piemēru izmantosim Mega Millions. Iespēja laimēt džekpotu šeit ir 1 pret 302 575 350, t. i., 0,00000033049619%. Otrs faktors ir džekpota lielums, kas, protams, atšķiras. Nākamajā tabulā ir parādīts, kā jūsu EV ir atkarīgs no džekpota lieluma.Megamillions džekpota EV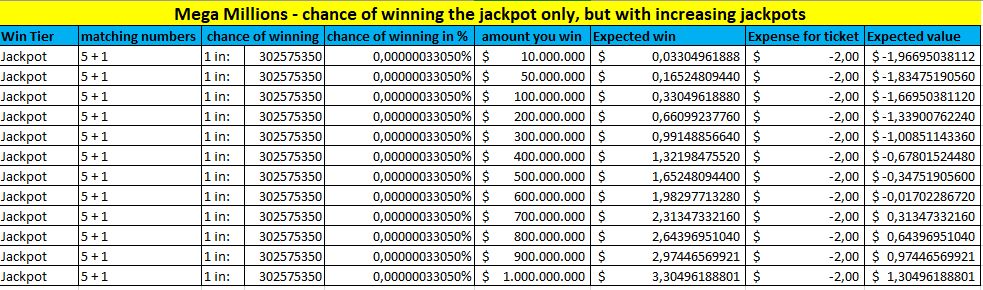
Tas ir interesanti, vai ne? Jūs redzat, ka matemātiski jūsu EV palielinās, jo lielāks ir džekpots. Patiesībā šajā tabulā redzams, ka, ja džekpota summa ir 700 miljoni ASV dolāru, jūsu EV ir aptuveni 0,31 ASV dolārs. Un šajā skaitlī pat nav ņemtas vērā jūsu izredzes vinnēt kādu no citām zemāko līmeņu balvām.
Tas ved mūs pie vēl vienas interesantas domas. Pieņemsim, ka džekpots ir 700 miljoni ASV dolāru un ir 302,575 miljoni iespējamo skaitļu kombināciju. Ko darīt, ja mēs nopirktu 302 575 miljonus biļešu par 2,00 $, lai aptvertu visas iespējamās skaitļu kombinācijas? Tas mums izmaksātu aptuveni 605 miljonus ASV dolāru, bet mums būtu garantēts 700 miljonu ASV dolāru laimests un visi mazie laimesti. Tam vajadzētu izdoties, vai ne? Diemžēl tas nedarbosies, pat ja jums būtu pietiekami daudz naudas, lai iegādātos tik daudz loterijas biļešu.
Tad kāpēc šī nav dzīvotspējīga stratēģija, lai katru reizi vinnētu?
Divi vienkārši iemesli:
- Nodokļi – ja jūs vinnēsiet, jums būs jāmaksā vismaz 30 % nodokļu par laimestu. Tas nozīmē, ka džekpotam ir jābūt vēl lielākam, nekā norādīts tabulā, lai jums būtu garantēta peļņa.
- Vairāki uzvarētāji sadalīs džekpotu – jums var būt garantēta džekpota vinnesta balva, bet ko darīt, ja laimīgie skaitļi būs vēl vienam vai diviem cilvēkiem? Jums džekpots būs jāsadala, bet vinnesta summa nav garantēta. Un vēl ir jautājums par nodokļiem.
Lielāko loteriju paredzamās vērtības salīdzinājums
Tagad apskatīsim, kuras loterijas piedāvā “labāko piedāvājumu” par jūsu naudu. Mēs salīdzināsim mūsu visvairāk pārdotās loterijas – Mega Millions, Powerball, Euromillions un Eurojackpot. Lai varētu sniegt godīgu salīdzinājumu, pieņemsim, ka džekpots ir vienāds visās loterijās – 100 miljoni.
Tagad ņemsim vērā arī visus laimestu līmeņus un to varbūtības, kā arī vidējo summu, ko var sagaidīt katrā līmenī.
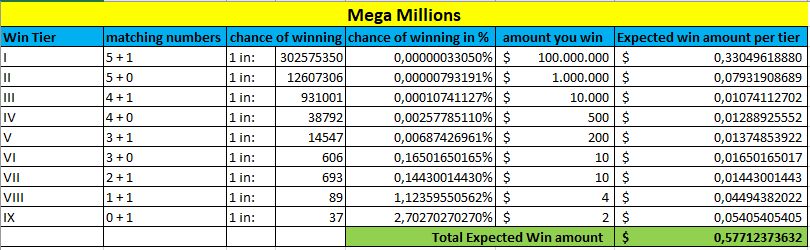
Katras tabulas apakšdaļā, kas atzīmēta zaļā krāsā, ir redzama paredzamā laimesta summa. Jo lielāka ir šī summa, jo lielākas ir jūsu izredzes laimēt šajā loterijā.
Mega Millions
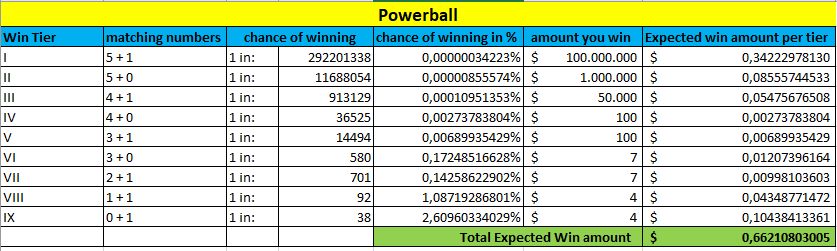
Powerball
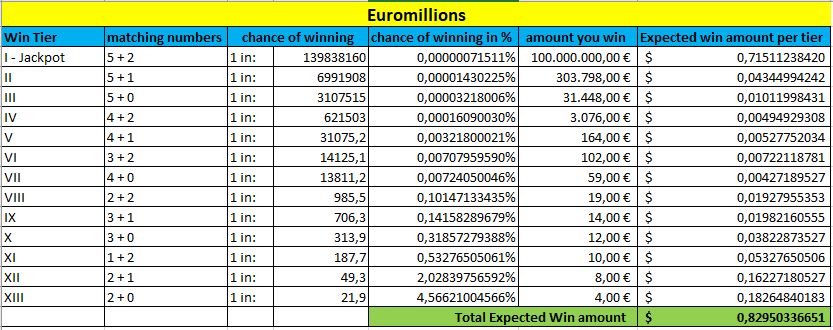
Euromillions
Eurojackpot
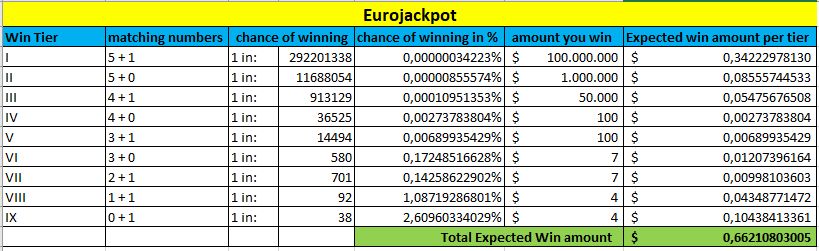
Arī šajā gadījumā viss mainās, kad palielinās džekpoti. Tomēr iepriekš sniegtajā tabulā ir sniegts labs loteriju salīdzinājums kopumā, pamatojoties uz jūsu izredzēm laimēt kādu no balvām.
Secinājums
Ne visas loterijas piedāvā vienādas izredzes laimēt. Lai gan dažādas loterijas būtībā darbojas vienādi, katrai loterijai ir atšķirīga izmaksu un laimestu struktūra.
Taču galu galā ir skaidrs, ka, jo lielāks ir laimests, jo vairāk iemeslu jums ir iegādāties biļeti un piedalīties loterijā!
