De faktorer, der definerer din chance for at vinde i lotteriet

I denne artikel vil vi forklare:

• hvordan lotterier fungerer
• hvordan lotterier genererer overskud
• hvad dine chancer er for at vinde en bestemt præmie i lotteriet
• hvordan matematikken bag lotteriet fungerer
• begrebet profitforventning, også kendt som forventet værdi
• hvordan man tager alle disse faktorer i betragtning, når man skal beslutte, hvilket lotteri man skal spille, og hvornår man skal købe en lodseddel

Hvordan genererer lotterier overskud?

Kort sagt giver alle lotterier overskud ved at sørge for, at kun en procentdel af de penge, der kommer ind gennem billetsalget, bliver udbetalt i form af gevinster. For at skabe overskud skal udbetalingerne i alle de vindende niveauer overvejes, fra jackpotten ned til den mindste mulige gevinst.

De fleste statsdrevne lotterier har relativt høje marginer. De to hovedårsager til det er:

1. De har relativt høje drifts- og administrationsomkostninger
2. Deres overskud bruges til at støtte alle former for velfærdsprojekter eller andre bestræbelser, der er i offentlighedens interesse. Det kan være amatørsport, miljøprojekter osv. I stedet for at bruge skatteindtægter til at finansiere sådanne projekter, afholder stater ofte lotterier for at skaffe de nødvendige midler. Man kan endda sige, at lotterier er en form for “frivillig” beskatning.

Hvad definerer chancerne for at vinde for spillerne?

Lad os se på matematikken bag begrebet lotteri. I hvert vindende lag er dine chancer defineret af antallet af mulige udfald af lodtrækningen, eller oddsene. Disse odds angives ofte som 1 ud af X – X er antallet af mulige udfald. Men ved at dividere 1 med X, kan du også få oddsene som en procentdel.

Hvis du for eksempel slår med en terning, er der seks mulige udfald. Hvis du gætter på resultatet af et kast, har du en chance på 1 ud af 6. Du kan også dividere 1 med 6, og så får du 16,667% chance for at gætte det rigtige resultat.

Samtidig skal du også overveje det beløb, du kan vinde, og den pris, du betaler for at deltage. Lad os se nærmere på dette koncept.

Konceptet profitforventning eller forventet værdi

Lad mig bruge et simpelt eksempel til at forklare, hvad Expected Value er. Vi vil bruge forkortelsen EV her.

Lad os sige, at jeg slår plat og krone med en mønt og betaler dig 1 dollar, hver gang resultatet er krone. Men hver gang resultatet er plat, skal du betale mig $1. Hvis vi gjorde dette mange, mange gange, ville EV komme tæt på nul, ikke?

Men hvad nu, hvis jeg betaler dig 2 dollars, hver gang du vinder, og du betaler mig 1 dollar, hver gang du taber? Det ville betyde, at du ville få en fortjeneste i det lange løb. Hvis du slår plat og krone tusind gange, vil resultatet være cirka 500 gange krone (du vinder 1.000 dollars) og 500 gange plat (du taber 500 dollars). Det er en fortjeneste på 500 dollars for 1000 møntkast, eller 0,50 dollars pr. møntkast.

Hvordan kan vi anvende dette på lotteriet?

Hvis vi antager en fast billetpris (vi kan bruge $1 som prisen for en billet til lotteriet her), skal vi udregne det på følgende måde:

Den procentvise chance ganget med det beløb, du ville vinde = din forventede værdi.

Hvis vi vil vide, hvordan dette gælder for at vinde jackpotten, er det sådan, vi gør det. Lad os bruge Mega Millions som et eksempel. Oddsene for at vinde jackpotten her er 1 i 302.575.350, hvilket betyder en procentdel på 0,00000033049619%. Den anden faktor er jackpottens størrelse, som selvfølgelig varierer. Følgende tabel viser, hvordan din EV afhænger af jackpottens størrelse.Megamillions jackpot EV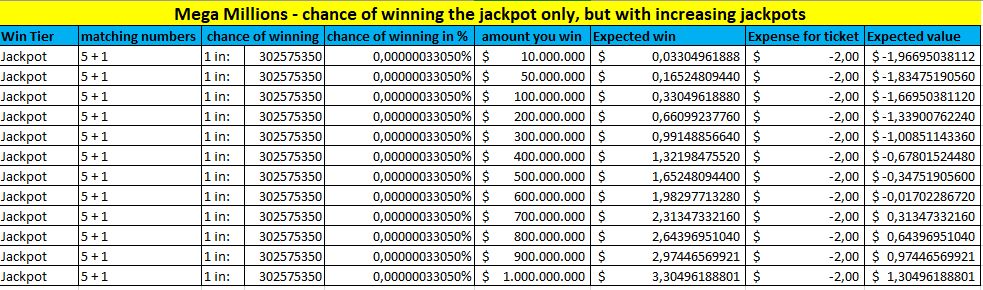

Det er interessant, ikke? Du kan se, at matematisk set stiger din EV, når jackpotten stiger. Faktisk kan du i tabellen se, at når jackpotten er på 700 millioner dollars, er din EV ca. 0,31 dollars. Og dette tal tager ikke engang højde for dine chancer for at vinde nogen af de andre præmier i de lavere niveauer.

Det fører os til en anden interessant tanke. Hvis vi antager, at jackpotten er på 700 millioner dollars, og der er 302,575 millioner mulige talkombinationer. Hvad nu, hvis vi skulle købe 302,575 millioner kuponer til en pris af $2,00 for at dække alle mulige talkombinationer? Det ville koste os ca. 605 millioner dollars, men vi ville have en garanteret gevinst på 700 millioner dollars plus alle de mindre gevinster. Det burde fungere, ikke? Desværre vil det ikke fungere, selv hvis du havde pengene til at købe så mange lodsedler.

Så hvorfor er dette ikke en brugbar strategi til at vinde hver gang?

Af to simple grunde:

• Skatter – hvis du vinder, skal du betale mindst 30% i skat af din gevinst. Det betyder, at jackpotten skal være endnu højere, end hvad tabellen antyder, for at du kan få en garanteret fortjeneste.
• Flere vindere skal dele jackpotten – du er måske garanteret at vinde jackpotten, men hvad hvis en eller to personer mere har vindertallene? Så bliver du nødt til at dele jackpotten, men det beløb, du vinder, er ikke garanteret. Og så er der stadig skattespørgsmålet.

Sammenligning af den forventede værdi for de største lotterier

Nu vil vi se på, hvilke lotterier der giver den “bedste deal” for dine penge. Vi vil sammenligne vores bedst sælgende lotterier, som er Mega Millions, Powerball, Euromillions og Eurojackpot. For at kunne give en retfærdig sammenligning vil vi antage, at jackpotten er den samme for hvert lotteri, nemlig 100 millioner.

Nu vil vi også tage højde for alle præmieniveauer og deres sandsynligheder, kombineret med det gennemsnitlige beløb, du kan forvente i hvert niveau.

I bunden af hver tabel, markeret med grønt, kan du se det forventede gevinstbeløb. Jo højere dette beløb er, jo bedre er dine chancer for at vinde dette lotteri.

Mega Millions

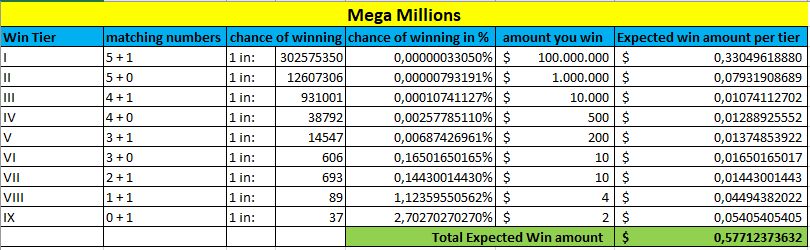
Powerball

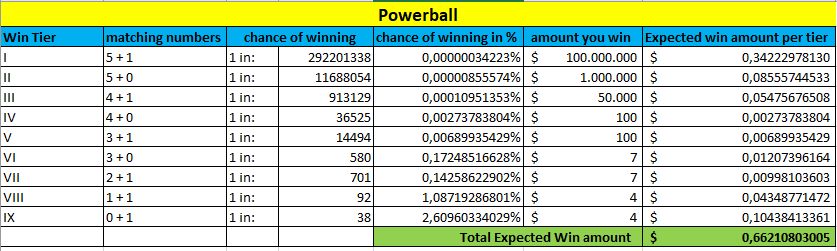
Euromillions

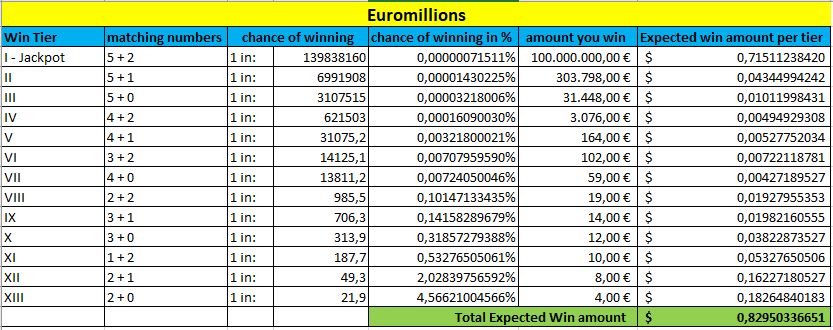
Eurojackpot

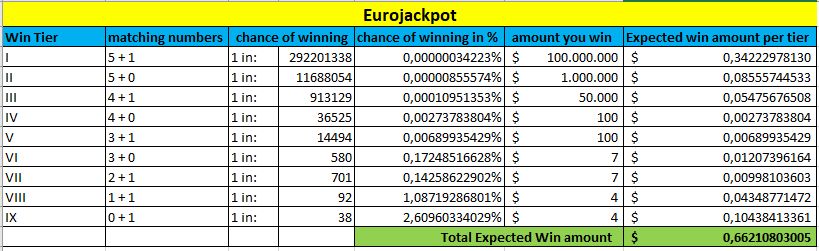
Igen ændrer alt dette sig, når jackpotterne stiger. Men ovenstående tabel giver dig en god sammenligning af lotterierne generelt, baseret på dine odds for at vinde en præmie.

Konklusion

Ikke alle lotterier tilbyder de samme odds for at vinde. Selvom de forskellige lotterier grundlæggende fungerer på samme måde, har hvert lotteri en forskellig struktur for udbetalinger og gevinster.

Men når alt kommer til alt, er der én ting, der giver mening: Jo højere jackpotten er, jo mere grund har du til at købe en kupon og deltage i lotteriet!